题目内容
如图正方体ABCD-A1B1C1D1中，M是正方形ABCD的中心，则直线A1D与直线B1M所成角大小为
- A.300
- B.450
- C.600
- D.900
A
分析：先将A1D平移到B1C，连接MC，得到的锐角∠MB1C就是异面直线所成的角，在三角形中再利用余弦定理求出此角即可．
解答：
解：如图，将A1D平移到B1C，连接MC，则∠MB1C是直线A1D与直线B1M所成角
设棱长为2，则B1C=
，MC=
，B1M=
cos∠MB1C=
，
∴∠MB1C=30°，
故选A．
点评：本小题主要考查异面直线所成的角，考查空间想象能力，运算能力和推理论证能力，属于基础题．
分析：先将A1D平移到B1C，连接MC，得到的锐角∠MB1C就是异面直线所成的角，在三角形中再利用余弦定理求出此角即可．
解答：
解：如图，将A1D平移到B1C，连接MC，则∠MB1C是直线A1D与直线B1M所成角设棱长为2，则B1C=
，MC=，B1M=cos∠MB1C=
，∴∠MB1C=30°，
故选A．
点评：本小题主要考查异面直线所成的角，考查空间想象能力，运算能力和推理论证能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
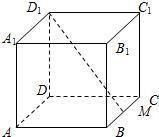如图正方体ABCD-A1B1C1D1中，M为BC中点，则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1的棱长为1，点M是棱AA1的中点，点O是BD1的中点，求证：OM是异面直线AA1，BD1的公垂线，并求OM的长．
如图正方体ABCD-A1B1C1D1的棱长为2，则点B1到直线AC的距离是
（文）如图正方体ABCD-A1B1C1D1，在它的12条棱及12条面的对角线所在的直线中，选取若干条直线确定平面，在所有的这些平面中：
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=