题目内容
 (2013•惠州一模)如图,ABC-A1B1C1中,侧棱与底面垂直,AB⊥AC,AB=AC=AA1=2,点M,N分别为A1B和B1C1的中点.
(2013•惠州一模)如图,ABC-A1B1C1中,侧棱与底面垂直,AB⊥AC,AB=AC=AA1=2,点M,N分别为A1B和B1C1的中点.(1)证明:MN∥平面A1ACC1;
(2)求二面角N-MC-A的正弦值.
分析:(1)如图所示,取A1B1的中点P,连接MP,NP.利用三角形的中位线定理可得NP∥A1C1,MP∥B1B;再利用线面平行的判定定理可得NP∥平面A1ACC1;MP∥平面A1ACC1;利用面面平行的判定定理可得平面MNP∥平面A1ACC1;进而得到线面平行MN∥平面A1ACC1;
(2)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出.
(2)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出.
解答:解:(1)如图所示, 取A1B1的中点P,连接MP,NP.
取A1B1的中点P,连接MP,NP.
又∵点M,N分别为A1B和B1C1的中点,∴NP∥A1C1,MP∥B1B,
∵NP?平面MNP,A1C1?平面MNP,∴NP∥平面A1ACC1;
同理MP∥平面A1ACC1;
又MP∩NP=P,
∴平面MNP∥平面A1ACC1;
∴MN∥平面A1ACC1;
(2)侧棱与底面垂直可得A1A⊥AB,A1A⊥AC,及AB⊥AC,可建立如图所示的空间直角坐标系.
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,2),B1(2,0,2),C1(0,2,2),N(1,1,2),M(1,0,1).
∴
=(-1,2,-1),
=(1,-1,2),
=(0,2,0).
设平面ACM的法向量为
=(x1,y1,z1),则
,令x1=1,则z1=-1,y1=0.
∴
=(1,0,-1).
设平面NCM的法向量为
=(x2,y2,z2),则
,令x2=3,则y2=1,z2=-1.
∴
=(3,1,-1).
∴cos<
,
>=
=
=
.
设二面角N-MC-A为θ,则sinθ=
=
=
.
故二面角N-MC-A的正弦值为
.
 取A1B1的中点P,连接MP,NP.
取A1B1的中点P,连接MP,NP.又∵点M,N分别为A1B和B1C1的中点,∴NP∥A1C1,MP∥B1B,
∵NP?平面MNP,A1C1?平面MNP,∴NP∥平面A1ACC1;
同理MP∥平面A1ACC1;
又MP∩NP=P,
∴平面MNP∥平面A1ACC1;
∴MN∥平面A1ACC1;
(2)侧棱与底面垂直可得A1A⊥AB,A1A⊥AC,及AB⊥AC,可建立如图所示的空间直角坐标系.
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,2),B1(2,0,2),C1(0,2,2),N(1,1,2),M(1,0,1).
∴
| MC |
| CN |
| AC |
设平面ACM的法向量为
| n1 |
|
∴
| n1 |
设平面NCM的法向量为
| n2 |
|
∴
| n2 |
∴cos<
| n1 |
| n2 |
|
| ||||
|
|
| 3+1 | ||||
|
2
| ||
| 11 |
设二面角N-MC-A为θ,则sinθ=
1-cos2<
|
1-(
|
| ||
| 11 |
故二面角N-MC-A的正弦值为
| ||
| 11 |
点评:本题综合考查了线面平行、面面平行、二面角、三角形的中位线定理、平面的法向量等基础知识,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
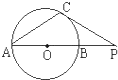 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题)