题目内容
已知f(x)=-2sin2x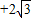 sinxcosx+5
sinxcosx+5(1)将函数化为f(x)=Asin(ωx+φ)+k(其中A>0,ω>0,0≤φ<2π)的形式,并指出函数f(x)的最小正周期;
(2)当x∈[
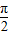 ,π]时,求f(x)的范围.
,π]时,求f(x)的范围.
【答案】分析:(1)利用二倍角公式、两角差的正弦函数化简函数为一个角的一个三角函数的形式,直接利用周期公式直接求函数f(x)的最小正周期.
(2)由(1)知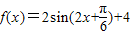 ,当x∈[
,当x∈[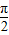 ,π]时,求出
,π]时,求出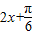 的范围,进而得到f(x)的范围.
的范围,进而得到f(x)的范围.
解答:解:(1)由于f(x)=-2sin2x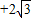 sinxcosx+5
sinxcosx+5
=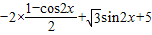
=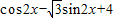
=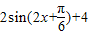
则函数f(x)的最小正周期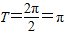
(2)由(1)知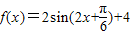 ,
,
∵x∈[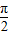 ,π],∴
,π],∴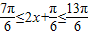
∴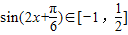 ,故f(x)∈[2,5]
,故f(x)∈[2,5]
∴f(x)的范围为[2,5].
点评:本题考查三角函数的化简,二倍角公式与两角和的正弦公式的应用,考查三角函数的周期性以及三角函数的值域,计算能力.
(2)由(1)知
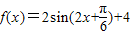 ,当x∈[
,当x∈[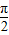 ,π]时,求出
,π]时,求出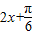 的范围,进而得到f(x)的范围.
的范围,进而得到f(x)的范围.解答:解:(1)由于f(x)=-2sin2x
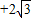 sinxcosx+5
sinxcosx+5=
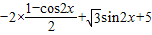
=
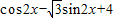
=
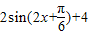
则函数f(x)的最小正周期
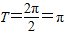
(2)由(1)知
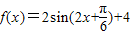 ,
,∵x∈[
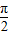 ,π],∴
,π],∴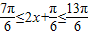
∴
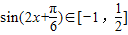 ,故f(x)∈[2,5]
,故f(x)∈[2,5]∴f(x)的范围为[2,5].
点评:本题考查三角函数的化简,二倍角公式与两角和的正弦公式的应用,考查三角函数的周期性以及三角函数的值域,计算能力.

练习册系列答案
相关题目