题目内容
设P为圆x2+y2=1上的动点,过P作x轴的垂线,垂足为Q,若 =λ
=λ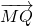 ,(其中λ为正常数),则点M的轨迹为
,(其中λ为正常数),则点M的轨迹为
- A.圆
- B.椭圆
- C.双曲线
- D.抛物线
B
分析:设M(x,y),P(x0,y0),则Q(x0,0),由由 =λ
=λ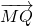 可得到x2+(λ+1)2y2=1.由此可知M的轨迹是椭圆.
可得到x2+(λ+1)2y2=1.由此可知M的轨迹是椭圆.
解答:设M(x,y),P(x0,y0),则Q(x0,0),
∴ ,
, ,
,
由 =λ
=λ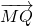
得 (λ>0)
(λ>0)
∴
由于x02+y02=1,∴x2+(λ+1)2y2=1.
∴M的轨迹是椭圆.
故选B.
点评:本题考查轨迹方程的求法,解题时要认真审题,仔细解答.
分析:设M(x,y),P(x0,y0),则Q(x0,0),由由
 =λ
=λ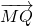 可得到x2+(λ+1)2y2=1.由此可知M的轨迹是椭圆.
可得到x2+(λ+1)2y2=1.由此可知M的轨迹是椭圆.解答:设M(x,y),P(x0,y0),则Q(x0,0),
∴
 ,
, ,
,由
 =λ
=λ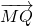
得
 (λ>0)
(λ>0)∴

由于x02+y02=1,∴x2+(λ+1)2y2=1.
∴M的轨迹是椭圆.
故选B.
点评:本题考查轨迹方程的求法,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
设P为圆x2+y2=1上的动点,过P作x轴的垂线,垂足为Q,若
=λ
,(其中λ为正常数),则点M的轨迹为( )
| PM |
| MQ |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |