题目内容
F1,F2为椭圆
+
=1(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率e=
,则椭圆的方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由椭圆得定义,△AF1B的周长=4a,求出a,再求出c,最后计算出b.
解答:解:由椭圆的定义,4a=16,a=4,又e=
=
,∴c=2
,∴b2=a2-c2=4,
则椭圆的方程是
+
=1
故选D
| c |
| a |
| ||
| 2 |
| 3 |
则椭圆的方程是
| x2 |
| 16 |
| y2 |
| 4 |
故选D
点评:本题考查椭圆标准方程求解、简单几何性质.属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
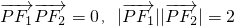 则m的值为________.
则m的值为________.