Question

（2013•深圳一模）已知Ω={（x，y）|x+y≤6，x≥0，y≥0}，A={（x，y）|x≤4，y≥0，x-y²≥0}，若向区域Ω上随机投一点P，则点P落入区域A的概率是

8

27

．

Answer 1

分析：作出Ω对应的平面区域，得到如图的Rt△OBC，其中B（6，0），C（0，6）．而A={（x，y）|x≤4，y≥0，x-y²≥0}表示的平面区域是在区域Ω内部，位于曲线y=

x

下方、直线x=4左边且在x轴上方的平面区域．利用定积分公式算出A对应的平面区域的面积S₁=

16

3

，再由Rt△OBC的面积为18，结合几何概型计算公式即可算出所求的概率．

解答：解：∵Ω={（x，y）|x+y≤6，x≥0，y≥0}，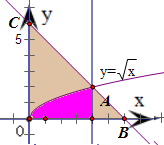
∴作出Ω对应的平面区域，得到如图的Rt△OBC，其中B（6，0），C（0，6）
又∵A={（x，y）|x≤4，y≥0，x-y²≥0}，
∴作出A对应的平面区域，得到曲线y=

x

下方、直线x=4左边，
且在x轴上方的平面区域，
其面积为S₁=

∫

4 0

x

dx=

2

3

x

3

2

|

4 0

=

2

3

×4

3

2

=

2

3

×8=

16

3

∵Rt_△OBC的面积为S=

1

2

×6×6=18
∴向区域Ω上随机投一点P，则点P落入区域A的概率P=

S1

S

=

16 3

18

=

8

27

故答案为：

8

27

点评：本题给出两个由不等式组确定的平面区域Ω和A，求向区域Ω内投点能使点落在A内的概率．着重考查了运用定积分公式计算曲边三角形的面积和几何概型计算公式等知识，属于中档题．