题目内容
在△ABC中,三个内角分别为A,B,C,且 .
.
(1)若 ,AC=3,求A、B.
,AC=3,求A、B.
(2)若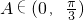 ,且
,且 ,求sinA.
,求sinA.
解:(1)在△ABC中,由 可得 sinB×
可得 sinB× +cosB×
+cosB× =2cosB,∴sinB=
=2cosB,∴sinB= cosB,∴tanB=
cosB,∴tanB= ,B=
,B= .
.
由 ,得 sinC=
,得 sinC= .
.
∴cosA=-cos(B+C)=-cosBcosC+sinBsinC=- +
+ =
= ,∴A=arccos
,∴A=arccos .
.
(2)若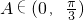 ,且
,且 ,则有 cos(
,则有 cos( -A)=
-A)= ,∴sin(
,∴sin( -A)=
-A)= .
.
∴sin(-A)=sin[( -A)-
-A)- )=sin(
)=sin( -A)cos
-A)cos -cos(
-cos( -A)sin
-A)sin =
= -
- =
= ,
,
故 sinA= .
.
分析:(1)在△ABC中,由 可得 tanB=
可得 tanB= ,B=
,B= .由
.由 ,得 sinC=
,得 sinC= .根据cosA=-cos(B+C),利用两角和差的余弦公式求得cosA,可得A的值.
.根据cosA=-cos(B+C),利用两角和差的余弦公式求得cosA,可得A的值.
(2)由条件求得 cos( -A)=
-A)= ,sin(
,sin( -A)=
-A)= .根据sin(-A)=sin[(
.根据sin(-A)=sin[( -A)-
-A)- ),利用两角差的正弦公式求得sin(-A)的值,即可求得 sinA 的值.
),利用两角差的正弦公式求得sin(-A)的值,即可求得 sinA 的值.
点评:本题主要考查两角和差的正弦、余弦公式的应用,同角三角函数的基本关系,属于中档题.
 可得 sinB×
可得 sinB× +cosB×
+cosB× =2cosB,∴sinB=
=2cosB,∴sinB= cosB,∴tanB=
cosB,∴tanB= ,B=
,B= .
.由
 ,得 sinC=
,得 sinC= .
.∴cosA=-cos(B+C)=-cosBcosC+sinBsinC=-
 +
+ =
= ,∴A=arccos
,∴A=arccos .
.(2)若
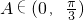 ,且
,且 ,则有 cos(
,则有 cos( -A)=
-A)= ,∴sin(
,∴sin( -A)=
-A)= .
.∴sin(-A)=sin[(
 -A)-
-A)- )=sin(
)=sin( -A)cos
-A)cos -cos(
-cos( -A)sin
-A)sin =
= -
- =
= ,
,故 sinA=
 .
.分析:(1)在△ABC中,由
 可得 tanB=
可得 tanB= ,B=
,B= .由
.由 ,得 sinC=
,得 sinC= .根据cosA=-cos(B+C),利用两角和差的余弦公式求得cosA,可得A的值.
.根据cosA=-cos(B+C),利用两角和差的余弦公式求得cosA,可得A的值.(2)由条件求得 cos(
 -A)=
-A)= ,sin(
,sin( -A)=
-A)= .根据sin(-A)=sin[(
.根据sin(-A)=sin[( -A)-
-A)- ),利用两角差的正弦公式求得sin(-A)的值,即可求得 sinA 的值.
),利用两角差的正弦公式求得sin(-A)的值,即可求得 sinA 的值.点评:本题主要考查两角和差的正弦、余弦公式的应用,同角三角函数的基本关系,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目