题目内容
（2013•通州区一模）已知x，y满足约束条件
，则z=x+y的最大值为
．
|
| 8 |
| 3 |
| 8 |
| 3 |
分析：要先根据约束条件画出可行域，再转化目标函数，把求目标函数的最值问题转化成求截距的最值问题．
解答：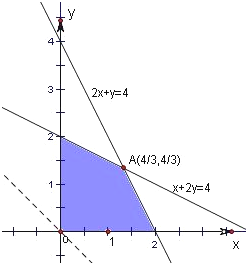
解：由约束条件画出可行域如图：
目标函数可化为y=-x+z，得到一簇斜率为-1，截距为z的平行线
要求z的最大值，须保证截距最大
由图象知，当目标函数的图象过点A是截距最大
又∵点A的坐标为（
，
）
∴z的最大值为
+
=
．
故答案为：
．
解：由约束条件画出可行域如图：目标函数可化为y=-x+z，得到一簇斜率为-1，截距为z的平行线
要求z的最大值，须保证截距最大
由图象知，当目标函数的图象过点A是截距最大
又∵点A的坐标为（
| 4 |
| 3 |
| 4 |
| 3 |
∴z的最大值为
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本题考查线性规划，须准确画出可行域．还要注意目标函数的图象与可行域边界直线的倾斜程度（斜率的大小）．属简单题
练习册系列答案
相关题目