题目内容
已知二次函数![]() 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为![]() 数列{
数列{![]() }的前n项和为
}的前n项和为![]() ,点
,点![]() 均在函数
均在函数![]() 的图像上.
的图像上.
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)设![]() ,
,![]() 的前n项和,求使得
的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m.
都成立的最小正整数m.
解:(I)设这二次函数![]() ,
,
由于![]() ,得
,得
![]()
又因为点![]() 的图像上,
的图像上,
所以![]()
当![]()
![]()
(II)由(I)得知![]()
![]()
故![]()
![]()
因此,要使![]() ,必须且仅须满足
,必须且仅须满足![]()
即![]() ,
,
所以满足要求的最小正整数m为10。

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 均在函数
均在函数 ,
,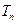 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.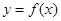 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为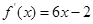 ,数列
,数列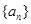 的前n项和为
的前n项和为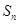 ,点
,点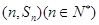 均在函数
均在函数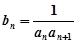 ,
, 是数列
是数列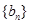 的前n项和,求使得
的前n项和,求使得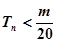 对所有
对所有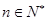 都成立的最小正整数m.
都成立的最小正整数m.