题目内容

函数f（x）=lnx+ln（2-x）+x的单调递增区间为

A.
$数学公式$
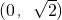
B.
$数学公式$
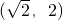
C.
（2，+∞）
D.
$数学公式$

A
分析：首先根据对数函数的性质求出定义域，再对函数f（x）=lnx+ln（2-x）+x进行求导，利用导数研究其极值问题；
解答：∵函数f（x）=lnx+ln（2-x）+x，可得0＜x＜2，
∴f′（x）= $\text{[math]}$ + $\text{[math]}$ +1= $\text{[math]}$ ，
∵0＜x＜2，∴x-2＜0，
若f′（x）＞0，可得 $\text{[math]}$ ＞0，
可得x²-2＜0，解得- $\text{[math]}$ ＜x＜ $\text{[math]}$ ，因为0＜x＜2，
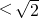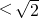∴0＜x $\text{[math]}$ ，此时f（x）为增函数，
故选A；
点评：此题主要考查利用导数研究函数的单调性及其应用，是一道中档题，解题过程中要注意函数f（x）的定义域，在定义域上研究函数的单调性才有意义；

练习册系列答案

新导航全程测试卷系列答案

新编初中总复习系列答案

校园英语英语大课堂系列答案

小状元金考卷单元考点梳理系列答案

小学总复习冲刺卷系列答案

小学总复习教程系列答案

通城学典小学总复习系列答案

小学综合能力测评同步训练系列答案

名师伴你总复习系列答案

步步通优系列答案

相关题目

已知函数f（x）=lnx-

；
（Ⅰ）当a＞0时，判断f（x）在定义域上的单调性；
（Ⅱ）求f（x）在[1，e]上的最小值．

7、函数f（x）=lnx-2x+3零点的个数为（　　）

已知定义在（0，+∞）上的三个函数f（x）=lnx，g（x）=x²-af（x），h（x）=x-a

且g（x）在x=1处取得极值．求a的值及函数h（x）的单调递增区间．

已知函数f（x）=

（k为常数，e=2.71828…是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与x轴平行．
（Ⅰ）求k的值；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=（x²+x）f′（x），其中f′（x）是f（x）的导函数．证明：对任意x＞0，g（x）＜1+e^-2．

已知函数f（x）=lnx-x
（1）求f（x）的单调区间；
（2）若不等式af（x）≥x-

x²在x∈（0，+∞）内恒成立，求实数a的取值范围；
（3）n∈N⁺，求证：