题目内容
设定义在R上的函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R),当x=-1时f(x)取得极大值 ,且函数y=f(x)为奇函数.
,且函数y=f(x)为奇函数.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设 ,求证:
,求证: .
.
(本小题满分13分)
解:(Ⅰ) 由f(x)为奇函数知 b=d=0…2′
又f′(-1)=0且f(-1)= ∴f(x)=
∴f(x)=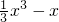 …4′
…4′
(Ⅱ)由(Ⅰ)知f′(x)=x2-1
∵ ,
, …6′
…6′
因为当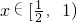 时,f′(x)=x2-1<0,即函数f(x)在
时,f′(x)=x2-1<0,即函数f(x)在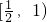 上递减∴
上递减∴ ,即
,即 …8′
…8′
又 ,
, …10′
…10′
又因为当 时,f′(x)=x2-1>0,即函数f(x)在
时,f′(x)=x2-1>0,即函数f(x)在 上递增;
上递增;
当 时,f′(x)=x2-1<0,即函数f(x)在
时,f′(x)=x2-1<0,即函数f(x)在 上递减
上递减
∵ ,
, ∴
∴
∴ ,
,
即: …12′
…12′
∴ …13′
…13′
分析:(Ⅰ)通过函数y=f(x)为奇函数,求出 b=d=0,当x=-1时f(x)取得极大值,导数为0,求出a,c,即可求函数f(x)的表达式;
(Ⅱ)求出函数的导数,求出xn的范围,推出 ,类比求出
,类比求出 ,即
,即 ,即可求证:
,即可求证: .
.
点评:本题考查函数的导数的应用,导数的极值、单调性,函数的解析式的求法,以及不等式的证明.难度较大,考查转化思想,计算能力.
解:(Ⅰ) 由f(x)为奇函数知 b=d=0…2′
又f′(-1)=0且f(-1)=
 ∴f(x)=
∴f(x)=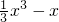 …4′
…4′(Ⅱ)由(Ⅰ)知f′(x)=x2-1
∵
 ,
, …6′
…6′因为当
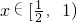 时,f′(x)=x2-1<0,即函数f(x)在
时,f′(x)=x2-1<0,即函数f(x)在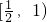 上递减∴
上递减∴ ,即
,即 …8′
…8′又
 ,
, …10′
…10′又因为当
 时,f′(x)=x2-1>0,即函数f(x)在
时,f′(x)=x2-1>0,即函数f(x)在 上递增;
上递增;当
 时,f′(x)=x2-1<0,即函数f(x)在
时,f′(x)=x2-1<0,即函数f(x)在 上递减
上递减∵
 ,
, ∴
∴
∴
 ,
,即:
 …12′
…12′∴
 …13′
…13′分析:(Ⅰ)通过函数y=f(x)为奇函数,求出 b=d=0,当x=-1时f(x)取得极大值,导数为0,求出a,c,即可求函数f(x)的表达式;
(Ⅱ)求出函数的导数,求出xn的范围,推出
 ,类比求出
,类比求出 ,即
,即 ,即可求证:
,即可求证: .
.点评:本题考查函数的导数的应用,导数的极值、单调性,函数的解析式的求法,以及不等式的证明.难度较大,考查转化思想,计算能力.

练习册系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |