题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)求极值,可先求得导数![]() ,然后通过解不等式
,然后通过解不等式![]() 确定增区间,解不等式
确定增区间,解不等式![]() 确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记
确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记![]() ,求出其导数
,求出其导数![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,这是
,这是![]() 时最小值,
时最小值,![]() ,这是
,这是![]() 时的最大值,因此要证明题中不等式,可分类,
时的最大值,因此要证明题中不等式,可分类,![]() 和
和![]() 分别证明.
分别证明.
试题解析:(1)依题意,![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ; 令
; 令![]() ,则
,则![]() ,
,
故当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]()
(2)由(1)知![]() ,令
,令![]() ,
,
则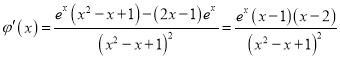 ,
,
可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,令
上单调递减,令![]() .
.
① 当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的图象在
的图象在![]() 图象的上方.
图象的上方.
② 当![]() 时,函数
时,函数![]() 单调递减,所以其最小值为
单调递减,所以其最小值为![]() 最大值为2,而
最大值为2,而![]() ,所以函数
,所以函数![]() 的图象也在
的图象也在![]() 图象的上方.
图象的上方.
综上可知,当![]() 时,
时,![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目