题目内容
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求方程有实根的概率.
三个数中任取的一个数,求方程有实根的概率.
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,其中
任取的一个数,其中 满足
满足 ,求方程有实根的概率,并求出其概率的最大值.
,求方程有实根的概率,并求出其概率的最大值.
【答案】
(1)  ;(2)
;(2)  , 所以其概率的最大值为
, 所以其概率的最大值为 .
.
【解析】(1) 总的基本事件有 个, 设事件A为“方程有实根”包含9个基本事件.
个, 设事件A为“方程有实根”包含9个基本事件.
所以事件A的概率为 .
.
(2)本小题属于几何概型.a,b构成的实数对(a,b)满足条件有  设事件B为“方程有实根”,则此事件满足几何概型
设事件B为“方程有实根”,则此事件满足几何概型
解:(1) 总的基本事件有 个,即a,b构成的实数对(a,b)有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),设事件A为“方程有实根”,包含的基本事件有(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个,所以事件A的概率为
个,即a,b构成的实数对(a,b)有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),设事件A为“方程有实根”,包含的基本事件有(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个,所以事件A的概率为 5分
5分
(2) a,b构成的实数对(a,b)满足条件有  设事件B为“方程有实根”,则此事件满足几何概型.
设事件B为“方程有实根”,则此事件满足几何概型.

因为 ,即
,即 所以
所以
即 所以其概率的最大值为
所以其概率的最大值为 12分
12分
 ,然后根据函数的方法求最值即可.
,然后根据函数的方法求最值即可.

练习册系列答案
相关题目
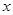 的一元二次方程
的一元二次方程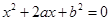 .
.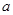 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,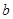 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率; 的一元二次方程
的一元二次方程 .
. 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率. 任取的一个数,
任取的一个数, 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率. 的一元二次方程
的一元二次方程 .
. 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率. 任取的一个数,
任取的一个数, 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率. 的一元二次方程
的一元二次方程 。
。 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率. 任取的一个数,
任取的一个数, 任取的一个数,
任取的一个数,