题目内容
已知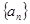 是等差数列,前n项和是
是等差数列,前n项和是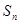 ,且
,且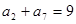 ,
,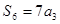 ,
,
(1)求数列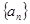 的通项公式;
的通项公式;
(2)令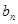 =
=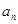 ·2n,求数列
·2n,求数列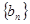 的前n项和
的前n项和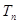
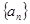 是等差数列,前n项和是
是等差数列,前n项和是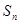 ,且
,且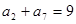 ,
,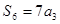 ,
,(1)求数列
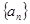 的通项公式;
的通项公式;(2)令
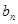 =
=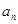 ·2n,求数列
·2n,求数列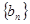 的前n项和
的前n项和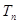
(1) ,(2)
,(2)
 ,(2)
,(2)
试题分析:(1)等差数列的求解方法为待定系数法,利用已知两个条件,列出关于首项及公差的方程组
 ,解出
,解出 ,从而可得数列
,从而可得数列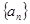 的通项公式
的通项公式 ;(2)数列求和,要先分析通项特征,本题是等差乘等比型,因此应用错位相减法求和. 设
;(2)数列求和,要先分析通项特征,本题是等差乘等比型,因此应用错位相减法求和. 设 ,则
,则 ,错位相减得
,错位相减得 ,再利用等比数列求和公式化简得
,再利用等比数列求和公式化简得
试题解析:
 解:(1)
解:(1)




解得
 4分
4分(2)

 ①
① ② 6分
② 6分① ②
 8分
8分所以:
 12分
12分
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
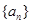 中,
中,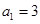 ,其前n项和为
,其前n项和为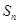 ,等比数列
,等比数列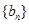 的各项均为正数,
的各项均为正数,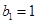 ,公比为q,且
,公比为q,且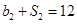 ,
,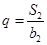 .
.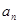 与
与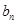 ;
;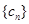 满足
满足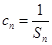 ,求
,求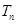 .
.