题目内容
已知函数![]() 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为![]() ,函数
,函数![]() 。
。
(1)若函数![]() 在
在![]() 处有极值,求
处有极值,求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间[-1,1]上为增函数,且
在区间[-1,1]上为增函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围。
的取值范围。
(1)∵![]() ,∴由
,∴由![]() =3得
=3得![]() ,
,
即切点坐标为![]()
∴切线方程为![]() ,或
,或![]() 2分
2分
整理得![]() 或
或![]()
∴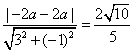 ,解得
,解得![]() ,∴
,∴![]() 。
。
∴![]() 4分
4分
∵![]() ,
,![]() 在
在![]() 处有极值,∴
处有极值,∴![]() ,
,
即![]() ,解得
,解得![]()
∴![]() 6分
6分
(2)∵函数![]() 在区间[-1,1]上为增函数,
在区间[-1,1]上为增函数,
∴![]() 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,
∴![]() 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,
∴![]() 8分
8分
即![]() ,若
,若![]() ,则不等式显然成立,若
,则不等式显然成立,若![]() ,
,
则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]()
故![]() 的取值范围是
的取值范围是![]() 12分
12分

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为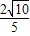 ,函数
,函数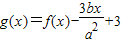 .
.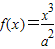 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为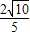 ,函数
,函数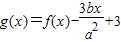 .
. 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为 ,函数
,函数 。
。 在
在 处有极值,求
处有极值,求 在
在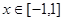 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。