题目内容
若集合A={y|y=2x，x∈R}，B={y|y=x2，x∈R}，则（ ）
分析：利用指数函数的单调性即可得到A={y|y＞0}；利用二次函数函数的单调性即可得到B={y|y≥0}；再利用集合之间的包含关系即可判断出．
解答：解：对于集合A：y=2x＞0，∴A={y|y＞0}；
对于集合B：y=x2≥0，∴B={y|y≥0}．
∴A?B．
故选A．
对于集合B：y=x2≥0，∴B={y|y≥0}．
∴A?B．
故选A．
点评：本题考查了指数函数的单调性、二次函数的单调性、集合之间的包含关系鞥基础知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若集合A={y|y=x3，0≤x≤1}，集合B={y|y=
，0＜x≤1}，则A∩CRB等于（ ）
| 1 |
| x |
| A、[0，1] | B、[0，1） |
| C、（1，+∞） | D、{1} |
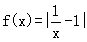
上的单调性，并证明你的结论；
}，B=[0,1]， 试判断A与B的关系；
}，B={y|y=3-x}，则A∪B=（ ）