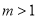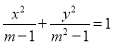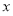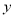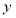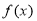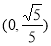题目内容
如图,矩形 所在的平面与正方形
所在的平面与正方形 所在的平面相互垂直,
所在的平面相互垂直, 是
是 的中点.
的中点.

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 .
.
(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)要证线面平行,只须在平面内找到一条直线与这条直线平行,对本小题来说,连接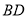 交
交 于点
于点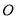 ,由三角形的中位线定理可证得
,由三角形的中位线定理可证得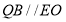 ,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形
,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形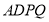 为正方形且
为正方形且 为对角线
为对角线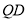 的中点,所以有
的中点,所以有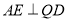 ,故可考虑证明
,故可考虑证明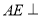 平面
平面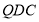 ,故需要在平面
,故需要在平面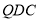 内再找一条直线与
内再找一条直线与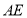 垂直即可,由平面
垂直即可,由平面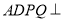 平面
平面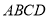 ,交线为
,交线为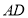 且
且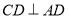 ,从而
,从而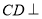 平面
平面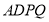 ,可得
,可得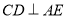 ,从而问题得证.
,从而问题得证.
试题解析:(1)连接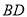 交
交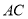 于
于 ,连接
,连接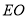

在三角形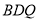 中,
中,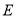 ,
, 分别为
分别为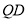 和
和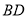 的中点
的中点
所以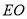 ∥
∥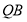 . 2分
. 2分
又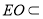 平面
平面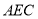 ,
,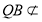 平面
平面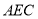
所以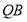 ∥平面
∥平面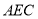 4分
4分
(2)因为矩形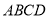 所在的平面与正方形
所在的平面与正方形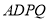 所在的平面相互垂直
所在的平面相互垂直
平面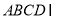 平面
平面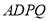 =
=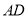 ,
,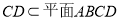 ,
,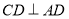
所以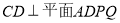
又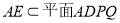 ,所以
,所以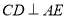 6分
6分
又因为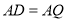 ,
,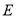 是
是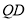 的中点,所以
的中点,所以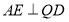
又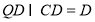 ,所以
,所以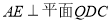 7分
7分
由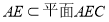 ,所以平面
,所以平面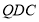 ⊥平面
⊥平面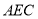 8分.
8分.
考点:1.线面平行的证明;2.面面垂直的判定与性质.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目