题目内容
已知二次函数f(x)=ax2+bx+1和函数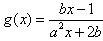 ,
,
(1)若f(x)为偶函数,试判断g(x)的奇偶性;
(2)若方程g(x)=x有两个不等的实根x1,x2(x1<x2),则
①函数f(x)在(-1,1)上是单调函数吗?说明理由;
②若方程f(x)=0的两实根为x3,x4(x3<x4),求使x3<x1<x2<x4成立的a的取值范围。
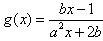 ,
,(1)若f(x)为偶函数,试判断g(x)的奇偶性;
(2)若方程g(x)=x有两个不等的实根x1,x2(x1<x2),则
①函数f(x)在(-1,1)上是单调函数吗?说明理由;
②若方程f(x)=0的两实根为x3,x4(x3<x4),求使x3<x1<x2<x4成立的a的取值范围。
解:(1)∵f(x)为偶函数,
∴ ,
,
∴bx=0,∴b=0,
∴ ,
,
∴函数g(x)为奇函数;
(2)①由 有不等实根,
有不等实根,
∴ ,
,
又f(x)的对称轴 ,
,
故f(x)在(-1,1)上是单调函数;
② 是方程(*)的根,
是方程(*)的根,
∴ ,
,
∴ ,
,
∴ ,
,
同理 ,
,
要使 ,
,
只需 ;
;
或 ;
;
故a的取值范围 。
。
∴
 ,
,∴bx=0,∴b=0,
∴
 ,
,∴函数g(x)为奇函数;
(2)①由
 有不等实根,
有不等实根,∴
 ,
,又f(x)的对称轴
 ,
,故f(x)在(-1,1)上是单调函数;
②
 是方程(*)的根,
是方程(*)的根,∴
 ,
,∴
 ,
,∴
 ,
,同理
 ,
,要使
 ,
,只需
 ;
;或
 ;
;故a的取值范围
 。
。 
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目