题目内容

设函数（x＞0且x≠1）
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）已知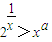对任意x∈（0，1）成立，求实数a的取值范围．
【答案】分析：（Ⅰ）求单调区间既是求函数导数大于或小于0的区间，我们可以用图表表示使结果直观．
（Ⅱ）对于未知数在指数上的式子，往往取对数进行解答．
解答：解：（Ⅰ），若f′（x）=0，则列表如下
x（1，+∞）
f′（x）+--
f（x）单调增极大值单调减单调减
（Ⅱ）在两边取对数，得，由于0＜x＜1，所以（1）
由（1）的结果可知，当x∈（0，1）时，，
为使（1）式对所有x∈（0，1）成立，当且仅当，即a＞-eln2
点评：求解此类问题要有耐心，避免不必要的计算错误．
练习册系列答案
相关题目
设函数g(x)=
x
+1，函数h(x)=
1
x+3
，x∈(-3，a]，其中a为常数且a＞0，令函数f（x）=g（x）•h（x）．
（1）求函数f（x）的表达式，并求其定义域；
（2）当a=
1
4
时，求函数f（x）的值域；
（3）是否存在自然数a，使得函数f（x）的值域恰为[
1
3
，
1
2
]？若存在，试写出所有满足条件的自然数a所构成的集合；若不存在，试说明理由．
（2013•潍坊一模）设函数f(x)=
1
3
mx3+(4+m)x2，g(x)=alnx，其中a≠0．
（ I ）若函数y=g（x）图象恒过定点P，且点P在y=f（x）的图象上，求m的值；
（Ⅱ）当a=8时，设F（x）=f′（x）+g（x），讨论F（x）的单调性；
（Ⅲ）在（I）的条件下，设G(x)=
f(x)，x≤1
g(x)，x＞1
，曲线y=G（x）上是否存在两点P、Q，使△OPQ（O为原点）是以O为直角顶点的直角三角形，且该三角形斜边的中点在y轴上？如果存在，求a的取值范围；如果不存在，说明理由．

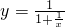设函数数学公式的定义域为M，值域为N，那么


  1. A.
    M={x|x≠0}，N={y|y≠0}
  2. B.
    M={x|x≠0}，N={y|y∈R}
  3. C.
    M={x|x＜0且x≠-1，或x＞0}，N={y|y＜0或0＜y＜1或y＞1}
  4. D.
    M={x|x＜-1或-1＜x＜0或x＞0}，N={y|y≠0}
设函数（x＞0且x≠1）。
（1）求函数f（x）的单调区间；
（2）已知对任意x∈（0，1）成立，求实数a的取值范围。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网