题目内容
已知函数 定义在
定义在 上,对于任意的
上,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
.
(1)验证函数 是否满足这些条件;
是否满足这些条件;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(3)若 ,试解关于
,试解关于 的方程
的方程 .
.
【答案】
(1)根据抽象函数定义可知, 满足条件。
满足条件。
(2)
【解析】
试题分析:解:(1)由 可得
可得 ,即其定义域为
,即其定义域为
又


又当 时,
时,


故 满足这些条件.
满足这些条件.
(2)令 ,
, ,令
,令 ,有
,有 ,
,
 为奇函数
为奇函数
由条件得 ,解得
,解得 .
.
(3)设 ,则
,则 ,
, ,
,
则 ,
, ,
,

 在
在 上是减函数
上是减函数

原方程即为 ,
,

又 故原方程的解为
故原方程的解为 .
.
考点:函数性质与方程解
点评:解决的关键是根据函数的性质以及方程的解的运用,属于中档题。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 是定义在
是定义在 上的偶函数,对于
上的偶函数,对于 都有
都有 成立,且
成立,且 ,当
,当 ,且
,且 时,都有
时,都有 >0.则给出下列命题:①
>0.则给出下列命题:① ;②函数
;②函数 的一条对称轴为
的一条对称轴为 ;③函数
;③函数 上为增函数;④方程
上为增函数;④方程 在
在 上有4个根。其中所有正确命题的序号是 。
上有4个根。其中所有正确命题的序号是 。 (其中
(其中 )是偶函数,则实数
)是偶函数,则实数 ;
; 既是奇函数又是偶函数;
既是奇函数又是偶函数; 的减区间是
的减区间是 ;
; 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足 ,则
,则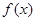 是定义在
是定义在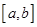 上的函数,其图象是一条连续的曲线,且满足下列条件:①
上的函数,其图象是一条连续的曲线,且满足下列条件:①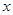 ,
,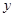 ∈
∈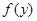 |<|
|<| 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 .对任意正数
.对任意正数 ,若
,若 ,则必有(
)
,则必有(
) B.
B.
 D.
D.