题目内容
.(本题14分)在数列 中,
中, ,
, ,
, .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
解:(Ⅰ)由已知
 --------------------5分
--------------------5分
又 --------------------6分
--------------------6分
所以,数列 是公比为4等比数列; --------------------7分
是公比为4等比数列; --------------------7分
(Ⅱ)由(Ⅰ) --------------------9分
--------------------9分
所以, --------------------11分
--------------------11分

--------------------------------------------14分
【解析】略

(本题14分)
 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | 0. 025 |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ ▲ ▲ ;
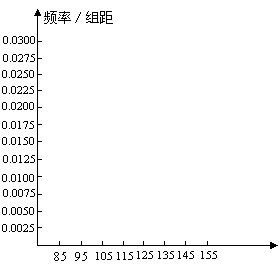
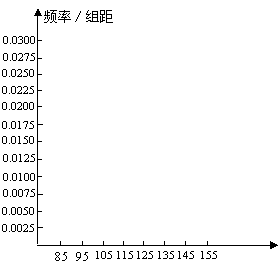
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
(本题14分)
 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | 0. 025 |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ 、 ▲ 、 ▲ ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
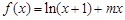
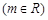 .
.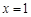 时,函数
时,函数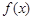 取得极大值,求实数
取得极大值,求实数 的值;
的值;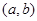 内存在导数,则存在
内存在导数,则存在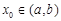 ,使得
,使得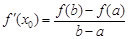 . 试用这个结论证明:若函数
. 试用这个结论证明:若函数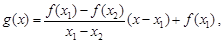 (其中
(其中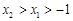 ),则对任意
),则对任意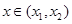 ,都有
,都有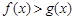 ;
;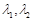 满足
满足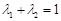 ,求证:对任意的实数
,求证:对任意的实数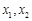 ,若
,若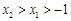 时,都有
时,都有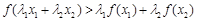 .
.