题目内容
下列函数中,既是奇函数又是增函数的是
- A.y=-x3
- B.y=cosx
- C.y=x|x|
- D.y=ex
C
分析:可利用函数的奇偶性的定义对A,B,C,D逐个判断即可.
解答:∵(-x)3=-x3,
∴y=-x3为奇函数,又y′=-3x2≤0,
∴y=-x3为R上的单调递减函数,可排除A;
∵cos(-x)=cosx
∴y=cosx为偶函数,可排除B;
对于D,y=ex为非奇非偶函数,
对于C,令y=f(x)=x|x|,
∵f(-x)=-x|-x|=-x|x|=-f(x),
∴y=f(x)=x|x|为奇函数,
又f(x)=x|x|=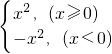 ,其图象如下:
,其图象如下:

由图象可知,f(x)=x|x|为R上的增函数.
∴C正确.
故选C.
点评:本题考查函数的奇偶性与单调性,着重考查排除法在解答选择题中的作用,考查分析与作图能力,属于中档题.
分析:可利用函数的奇偶性的定义对A,B,C,D逐个判断即可.
解答:∵(-x)3=-x3,
∴y=-x3为奇函数,又y′=-3x2≤0,
∴y=-x3为R上的单调递减函数,可排除A;
∵cos(-x)=cosx
∴y=cosx为偶函数,可排除B;
对于D,y=ex为非奇非偶函数,
对于C,令y=f(x)=x|x|,
∵f(-x)=-x|-x|=-x|x|=-f(x),
∴y=f(x)=x|x|为奇函数,
又f(x)=x|x|=
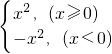 ,其图象如下:
,其图象如下:
由图象可知,f(x)=x|x|为R上的增函数.
∴C正确.
故选C.
点评:本题考查函数的奇偶性与单调性,着重考查排除法在解答选择题中的作用,考查分析与作图能力,属于中档题.

练习册系列答案
相关题目