题目内容
已知正方体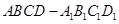 棱长为1,点
棱长为1,点 在
在 上,且
上,且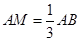 ,点
,点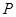 在平面
在平面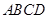 内,动点
内,动点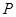 到直线
到直线 的距离与
的距离与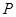 到点
到点 的距离的平方差等于1,则动点
的距离的平方差等于1,则动点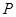 的轨迹是( )
的轨迹是( )
A. 圆 B. 抛物线 C. 双曲线 D. 直线
【答案】
B
【解析】
试题分析:作PN⊥AD,则PN⊥面A1D1DA,作 NH⊥A1D1 ,N,H为垂足则由三垂线定理可得 PH⊥A1D1.
以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M( ,0,0).
,0,0).
再由PN2+NH2=PH2,PH2-PM2=1,可得 PN2+NH2-PM2=1,
即 x2 +1-[(x-
 )2+(y-0)2]=1,化简可得y2=
)2+(y-0)2]=1,化简可得y2=  x-
x-  ,故答案为B
,故答案为B
考点:本题主要是考查点轨迹方程的求法。属于中档题.
点评:解决该试题的关键是得到 x2+1-[(x-
 )2+(y-0)2]=1,以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M(
)2+(y-0)2]=1,以AB,AD,AA1 为x轴,y轴,z轴,建立空间坐标系,设P(x,y,0),由题意可得 M( ,0,0),由题意可得(y2+1)-[(x-
,0,0),由题意可得(y2+1)-[(x-  )2+(y-0)2]=1,化简可得结果.
)2+(y-0)2]=1,化简可得结果.

练习册系列答案
相关题目
 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离. 棱长为1,点
棱长为1,点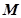 是
是 的中点,
的中点, 是
是 一动点,则
一动点,则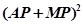 的最小值为______________.
的最小值为______________.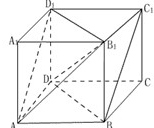 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离. 棱长为1,上底面A1B1C1D1的中心为O,P为棱
棱长为1,上底面A1B1C1D1的中心为O,P为棱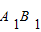 上的动点,则OP+AP的最小值为 .
上的动点,则OP+AP的最小值为 .