题目内容
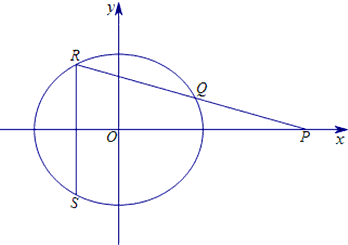 已知椭圆
已知椭圆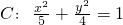 的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且
的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且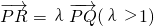 .
.
(1)若 ,求直线l的方程;
,求直线l的方程;
(2)试用λ表示Q点的横坐标,并求出λ的最大值;
(3)若点S是点R关于x轴的对称点,求证: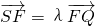 .
.
(1)解:设R(x1,y1),Q(x2,y2),则
∵ ,∴(x1-5,y1)=
,∴(x1-5,y1)= (x2-5,y2)
(x2-5,y2)
∴x1= x2-
x2- ,y1=
,y1= y2,
y2,
∵ ,
,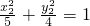
∴ ,
,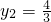
∵P(5,0),∴直线l的斜率为±
∴直线l的方程为y=± (x-5);
(x-5);
(2)解:∵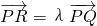 ,∴(x1-5,y1)=λ(x2-5,y2)
,∴(x1-5,y1)=λ(x2-5,y2)
∴x1=λx2-5λ+5,y1=λy2,
∵ ,
,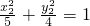
∴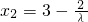
当且仅当P,Q,R在长轴上时,λ最大,此时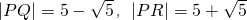 ,
,
∴λ=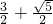
(3)证明:由(2)知,S(x1,-y1),F(1,0)
∴ =(1-x1,y1),
=(1-x1,y1), =(x2-1,y2),
=(x2-1,y2),
∵x1=λx2-5λ+5,y1=λy2,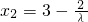
∴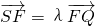
分析:(1)设R(x1,y1),Q(x2,y2),利用 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;
(2)利用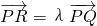 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;
(3)由(2)知,S(x1,-y1),F(1,0),用坐标表示向量,即可证得结论.
点评:本题考查直线与圆锥曲线的综合,考查向量知识的运用,解题的关键是确定坐标之间的关系.
∵
 ,∴(x1-5,y1)=
,∴(x1-5,y1)= (x2-5,y2)
(x2-5,y2)∴x1=
 x2-
x2- ,y1=
,y1= y2,
y2,∵
 ,
,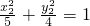
∴
 ,
,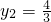
∵P(5,0),∴直线l的斜率为±

∴直线l的方程为y=±
 (x-5);
(x-5);(2)解:∵
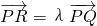 ,∴(x1-5,y1)=λ(x2-5,y2)
,∴(x1-5,y1)=λ(x2-5,y2)∴x1=λx2-5λ+5,y1=λy2,
∵
 ,
,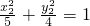
∴
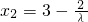
当且仅当P,Q,R在长轴上时,λ最大,此时
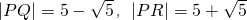 ,
,∴λ=
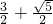
(3)证明:由(2)知,S(x1,-y1),F(1,0)
∴
 =(1-x1,y1),
=(1-x1,y1), =(x2-1,y2),
=(x2-1,y2),∵x1=λx2-5λ+5,y1=λy2,
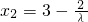
∴
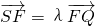
分析:(1)设R(x1,y1),Q(x2,y2),利用
 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,即可求得直线l的方程;(2)利用
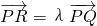 ,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;
,可得坐标之间的关系,再利用点在椭圆上,求得点的坐标,当且仅当P,Q,R在长轴上时,λ最大;(3)由(2)知,S(x1,-y1),F(1,0),用坐标表示向量,即可证得结论.
点评:本题考查直线与圆锥曲线的综合,考查向量知识的运用,解题的关键是确定坐标之间的关系.

练习册系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C