题目内容
15.已知等差数列{an}的前n项和为Sn,若an+an+1+an+2=18,S2n+1=54,则n的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 由等差数列的性质可得an+1=6,代入S2n+1=(2n+1)an+1=54,解方程可得.
解答 解:由题意和等差数列的性质可得an+an+1+an+2=3an+1=18,∴an+1=6,
再由等差数列的求和公式和性质可得S2n+1=(2n+1)an+1=6(2n+1)=54,
解关于n的方程可得n=4,
故选:C.
点评 本题考查等差数列的求和公式和性质,属基础题.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=2,AA′=1,点M,N分别为A′B和B′C′的中点.
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=2,AA′=1,点M,N分别为A′B和B′C′的中点. 的焦点为
的焦点为 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 两点.
两点. ,求直线
,求直线 的斜率;
的斜率; 在线段
在线段 上运动,原点
上运动,原点 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形 面积的最小值.
面积的最小值. 满足约束条件
满足约束条件 ,那么
,那么 的最大值是__________.
的最大值是__________.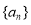 满足
满足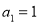 ,
,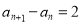 ,等比数列
,等比数列 满足
满足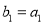 ,
, .
.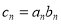 ,求数列
,求数列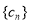 的前
的前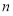 项和
项和 .
.