题目内容
已知函数
(1)求f(x)的单调递减区间;
(2)若f(x)向右平移m个单位(m>0)使得图象关于y轴对称,求m的最小值;
(3)若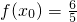 ,
,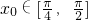 ,求cos2x0的值.
,求cos2x0的值.
解:(1) =2cosx(
=2cosx( cosx+
cosx+ sinx)-
sinx)- sin2x+
sin2x+ sin2x
sin2x
= cos2x+sin2x=
cos2x+sin2x= .
.
由 ,k∈Z,解得
,k∈Z,解得  ,k∈Z,
,k∈Z,
∴f(x)的单调递减区间为 ,k∈Z.
,k∈Z.
(2)f(x)右移m个单位后,得到函数为 ,由于图象关于y轴对称,
,由于图象关于y轴对称,
∴ ,k∈Z.∴
,k∈Z.∴ .
.
∵m>0,∴k=-1时, .
.
(3)∵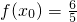 =
= ,∴
,∴ =
= ,又
,又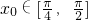 ,
,
故 ∈[
∈[ ,
, ],故cos(
],故cos( )=-
)=- .
.
cos2x0=cos[( )-
)- ]=cos(
]=cos( )cos
)cos +sin(
+sin( )sin
)sin =
=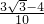 .
.
分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为 ,由
,由 求出x的范围,即得f(x)的单调递减区间.
求出x的范围,即得f(x)的单调递减区间.
(2)利用函数y=Asin(ωx+∅)的图象变换求出g(x)的解析式为 ,令
,令 ,k∈Z,
,k∈Z,
及m>0,求出m的最小值.
(3)由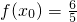 =
= ,解出
,解出 的值,并根据
的值,并根据 ∈[
∈[ ,
, ],求出cos(
],求出cos( ) 的值,由cos2x0=cos[(
) 的值,由cos2x0=cos[( )-
)- ]利用两角差的余弦公式求得结果.
]利用两角差的余弦公式求得结果.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调性,函数y=Asin(ωx+∅)的图象变换,属于中档题.
 =2cosx(
=2cosx( cosx+
cosx+ sinx)-
sinx)- sin2x+
sin2x+ sin2x
sin2x =
 cos2x+sin2x=
cos2x+sin2x= .
.由
 ,k∈Z,解得
,k∈Z,解得  ,k∈Z,
,k∈Z,∴f(x)的单调递减区间为
 ,k∈Z.
,k∈Z.(2)f(x)右移m个单位后,得到函数为
 ,由于图象关于y轴对称,
,由于图象关于y轴对称,∴
 ,k∈Z.∴
,k∈Z.∴ .
.∵m>0,∴k=-1时,
 .
.(3)∵
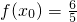 =
= ,∴
,∴ =
= ,又
,又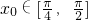 ,
,故
 ∈[
∈[ ,
, ],故cos(
],故cos( )=-
)=- .
.cos2x0=cos[(
 )-
)- ]=cos(
]=cos( )cos
)cos +sin(
+sin( )sin
)sin =
=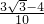 .
.分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为
 ,由
,由 求出x的范围,即得f(x)的单调递减区间.
求出x的范围,即得f(x)的单调递减区间.(2)利用函数y=Asin(ωx+∅)的图象变换求出g(x)的解析式为
 ,令
,令 ,k∈Z,
,k∈Z,及m>0,求出m的最小值.
(3)由
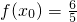 =
= ,解出
,解出 的值,并根据
的值,并根据 ∈[
∈[ ,
, ],求出cos(
],求出cos( ) 的值,由cos2x0=cos[(
) 的值,由cos2x0=cos[( )-
)- ]利用两角差的余弦公式求得结果.
]利用两角差的余弦公式求得结果.点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调性,函数y=Asin(ωx+∅)的图象变换,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

