题目内容
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b（0＜b＜A）的三个相邻交点的横坐标分别是2，4，8，则f（x）的单调递增区间是 ．
【答案】分析：求出函数的周期，即可求出ω，判断函数的最大值，通过正弦函数的图象性质，直接求出函数的单调增区间．
解答：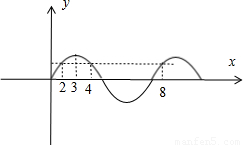
解：因为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象
与直线y=b（0＜b＜A）的三个相邻交点的横坐标分别是2，4，8，
所以函数的周期为：6，所以ω=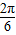
=
，
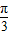并且函数的x=3时取得最大值，所以函数的单调增区间为：[6k，6k+3]（k∈Z）．
故答案为：[6k，6k+3]（k∈Z）．
点评：本题考查函数的解析式的求法，利用正弦函数的性质不求出函数的解析式，判断函数的单调增区间是解题本题解答的关键所在．
解答：
解：因为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b（0＜b＜A）的三个相邻交点的横坐标分别是2，4，8，
所以函数的周期为：6，所以ω=
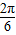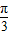=，并且函数的x=3时取得最大值，所以函数的单调增区间为：[6k，6k+3]（k∈Z）．
故答案为：[6k，6k+3]（k∈Z）．
点评：本题考查函数的解析式的求法，利用正弦函数的性质不求出函数的解析式，判断函数的单调增区间是解题本题解答的关键所在．
练习册系列答案
相关题目