题目内容
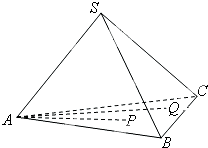如图，在三棱锥S-ABC中，设P、Q为底面△ABC内的两点，且| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| AQ |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| 4 |
| 5 |
| 4 |
| 5 |
分析：过P作AB、AC的平行线PD、PE，得到平行四边形ADPE，利用向量加法法则可得
=
+
，结合题意得到
=
且
=
，因此P到AB的距离等于点C到AB距离的
，所以△ABP的面积等于△ABC面积的
．同理△ABQ的面积等于△ABC面积的
，由此结合锥体体积公式即可算出VS-ABP：VS-ABQ的值．
| AP |
| AD |
| AE |
| AD |
| 1 |
| 5 |
| AC |
| AE |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 4 |
解答：解：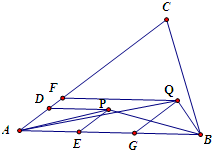
过P作AB、AC的平行线PD、PE得平行四边形ADPE
则向量
=
+
∵
=
+
，
∴由平面向量的基本定理，可得
=
且
=
因此，点P到AB的距离等于点C到AB距离的
∴
=
再过Q作AB、AC的平行线QF、QG得平行四边形AFQG
同理可证
=
且
=
，
可得点Q到AB的距离等于点C到AB距离的
，得
=
因此，△ABP的面积与△ABQ的面积之比为
∵VS-ABP=
S△ABP•d，VS-ABQ=
S△ABP•d．其中d为S到平面ABC的距离
∴VS-ABP：VS-ABQ=
故答案为：
过P作AB、AC的平行线PD、PE得平行四边形ADPE则向量
| AP |
| AD |
| AE |
∵
| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
∴由平面向量的基本定理，可得
| AD |
| 1 |
| 5 |
| AC |
| AE |
| 2 |
| 5 |
| AB |
因此，点P到AB的距离等于点C到AB距离的
| 1 |
| 5 |
∴
| S△ABP |
| S△ABC |
| 1 |
| 5 |
再过Q作AB、AC的平行线QF、QG得平行四边形AFQG
同理可证
| AF |
| 1 |
| 4 |
| AC |
| AG |
| 2 |
| 3 |
| AB |
可得点Q到AB的距离等于点C到AB距离的
| 1 |
| 4 |
| S△ABQ |
| S△ABC |
| 1 |
| 4 |
因此，△ABP的面积与△ABQ的面积之比为
| 4 |
| 5 |
∵VS-ABP=
| 1 |
| 3 |
| 1 |
| 3 |
∴VS-ABP：VS-ABQ=
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题给出三角形ABC内的点P、Q满足的条件，求两个锥体的体积之比．着重考查了平面向量加法法则、平面向量基本定理及其应用和锥体体积公式等知识，属于中档题．
练习册系列答案
相关题目
如图，在三棱锥S-ABC中，SA⊥平面ABC，平面SAB⊥平面SBC．
如图，在三棱锥S-ABC中，G1，G2分别是△SAB和△SAC的重心，则直线G1G2与BC的位置关系是（ ）
如图，在三棱锥S-ABC中，平面SBC⊥平面ABC，SB=SC=AB=2，BC=2
（2013•杭州模拟）如图，在三棱锥S-ABC中，SA=SC=AB=BC，则直线SB与AC所成角的大小是（ ）
（2013•成都一模）如图，在三棱锥S-ABC中，SA丄平面ABC，SA=3，AC=2，AB丄BC，点P是SC的中点，则异面直线SA与PB所成角的正弦值为（ ）