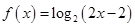题目内容
函数
 的部分图像可能是( )
的部分图像可能是( )
A. B. C. D.
A
解析试题分析:∵f(x)=x-sinx(x∈R)是奇函数,∴图象关于原点对称,∴排除D.
∵函数的导数为f'(x)=1-cosx≥0,∴函数f(x)在R上单调递增,∴排除C. ≈-0.57>-1,∴排除B,故选:A.
≈-0.57>-1,∴排除B,故选:A.
考点:函数的图象.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设函数 ,则( )
,则( )
A. 为 为 的极大值点 的极大值点 | B. 为 为 的极小值点 的极小值点 |
C. 为 为 的极大值点 的极大值点 | D. 为 为 的极小值点 的极小值点 |
已知函数f(x)满足f(x)=f(π-x),且当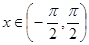 时,f(x)=x+sinx,则( )
时,f(x)=x+sinx,则( )
| A.f(1)<f(2)<f(3) | B.f(2)<f(3)<f(1) |
| C.f(3)<f(2)<f(1) | D.f(3)<f(1)<f(2) |
若函数 在区间
在区间 上存在一个零点,则
上存在一个零点,则 的取值范围是( )
的取值范围是( )
A. | B. 或 或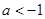 | C. | D.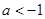 |
函数 与
与 的图像交点的横坐标所在区间为( )
的图像交点的横坐标所在区间为( )
A. | B. | C. | D. |
.函数 为偶函数,且在
为偶函数,且在 单调递增,则
单调递增,则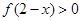 的解集为( )
的解集为( )
A. | B. |
C. | D. |
 满足:
满足: ,
, ,则方程
,则方程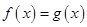 在区间
在区间 上的所有实根之和为( )
上的所有实根之和为( )



 图象中,满足
图象中,满足 的只可能是( )
的只可能是( )
 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数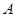 为函数
为函数