题目内容
（本小题满分12分）
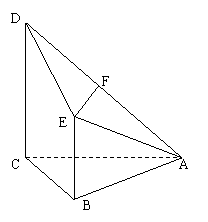已知四棱锥
，其中
，
，
，
∥
，
为
的中点.
（Ⅰ）求证：
∥面
；
（Ⅱ）求证：面
；
（III）求四棱锥的体积.
（本小题满分12分）
解：（Ⅰ）取AC中点G,连结FG、BG，
∵F,G分别是AD,AC的中点
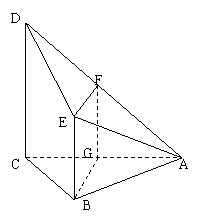∴FG∥CD,且FG=
DC=1 ．
∵BE∥CD ∴FG与BE平行且相等
∴EF∥BG． ……………………………2分
∴
∥面
……………………………4分
（Ⅱ）∵△ABC为等边三角形 ∴BG⊥AC
又∵DC⊥面ABC,BG
面ABC ∴DC⊥BG
∴BG垂直于面ADC的两条相交直线AC,DC，
∴BG⊥面ADC ． …………………………………………6分
∵EF∥BG
∴EF⊥面ADC
∵EF面ADE，∴面ADE⊥面ADC ． …………………………………………8分
（Ⅲ）连结EC,该四棱锥分为两个三棱锥E－ABC和E－ADC ．
．………………………12分
另法：取
的中点为
，连结
，则
，又
平面,
∴
, ∴
平面
，∴为
的高，
．
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
