题目内容
设函数 (
( ,
, 为自然对数的底数). 若存在
为自然对数的底数). 若存在 使
使 成立,则
成立,则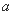 的取值范围是( )
的取值范围是( )
(A)  (B)
(B)  (C)
(C)  (D)
(D)
B

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
题目内容
设函数 (
( ,
, 为自然对数的底数). 若存在
为自然对数的底数). 若存在 使
使 成立,则
成立,则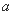 的取值范围是( )
的取值范围是( )
(A)  (B)
(B)  (C)
(C)  (D)
(D)
B

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案