题目内容
已知数列{an}为等比数列,其前n项和为Sn,已知a1+a4=-
,且S1,S3,S2成等差,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),记Tn=|
|+|
|+|
|+…+|
|,若(n-1)2≤m(Tn-n-1)对于n≥2,n∈N+恒成立,求实数m的取值范围.
| 7 |
| 16 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知bn=n(n∈N+),记Tn=|
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
分析:(I)利用等差数列和等比数列的通项公式即可得出;
(II)由bn=n,an=(-
)n,可得
=n•2n,利用“错位相减法”即可得到Tn.(n-1)2≤m(Tn-n-1)对于n≥2,n∈N+恒成立?m≥
对n≥2恒成立.通过研究右边的单调性即可得出.
(II)由bn=n,an=(-
| 1 |
| 2 |
| |bn| |
| |an| |
| n-1 |
| 2n+1-1 |
解答:解:(Ⅰ)设数列{an}的公比为q,
∵S1,S3,S2成等差,
∴2S3=S1+S2,
∴2a1(1+q+q2)=a1(2+q),得2q2+q=0,q≠0,解得q=-
.
又a1+a4=-
,a1+a1q3=-
,∴a1[1+(-
)3]=-
,解得a1=-
,
∴an=-
•(-
)n-1=(-
)n.
(Ⅱ)∵bn=n,an=(-
)n,∴
=n•2n.
∴Tn=1×2+2×22+3×23+…+n×2n,
2Tn=1×22+2×23+…+(n-1)×2n+n×2n+1,
∴-Tn=2+22+23+…+2n-n×2n+1=
-n•2n+1=(1-n)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
若(n-1)2≤m(Tn-n-1)对于n≥2,n∈N+恒成立,则(n-1)2≤m[(n-1)•2n+1+2-n-1],
∴m≥
对n≥2恒成立.
令f(n)=
,f(n+1)-f(n)=
-
=
<0,
∴当n≥2时,f(n+1)<f(n),f(n)为减函数,f(n)≤f(2)=
.∴m≥
.
∵S1,S3,S2成等差,
∴2S3=S1+S2,
∴2a1(1+q+q2)=a1(2+q),得2q2+q=0,q≠0,解得q=-
| 1 |
| 2 |
又a1+a4=-
| 7 |
| 16 |
| 7 |
| 16 |
| 1 |
| 2 |
| 7 |
| 16 |
| 1 |
| 2 |
∴an=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵bn=n,an=(-
| 1 |
| 2 |
| |bn| |
| |an| |
∴Tn=1×2+2×22+3×23+…+n×2n,
2Tn=1×22+2×23+…+(n-1)×2n+n×2n+1,
∴-Tn=2+22+23+…+2n-n×2n+1=
| 2×(2n-1) |
| 2-1 |
∴Tn=(n-1)•2n+1+2.
若(n-1)2≤m(Tn-n-1)对于n≥2,n∈N+恒成立,则(n-1)2≤m[(n-1)•2n+1+2-n-1],
∴m≥
| n-1 |
| 2n+1-1 |
令f(n)=
| n-1 |
| 2n+1-1 |
| n |
| 2n+2-1 |
| n-1 |
| 2n+1-1 |
| (2-n)•2n+1-1 |
| (2n+2-1)(2n+1-1) |
∴当n≥2时,f(n+1)<f(n),f(n)为减函数,f(n)≤f(2)=
| 1 |
| 7 |
| 1 |
| 7 |
点评:本题考查了等差数列和等比数列的通项公式、“错位相减法”、数列的单调性、恒成立问题的等价转化等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

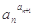 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4