Question

（2012年高考（四川文））已知为正实数,为自然数,抛物线与轴正半轴相交于点,设为该抛物线在点处的切线在轴上的截距.

(Ⅰ)用和表示;

(Ⅱ)求对所有都有成立的的最小值;

(Ⅲ)当时,比较与

的大小,并说明理由.

Answer 1

 (1)由已知得,交点A的坐标为,对

则抛物线在点A处的切线方程为:

 

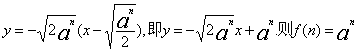
(2)由(1)知f(n)=,则

即知,对于所有的n成立,

特别地,当n=1时,得到a≥3

当a=3,n≥1时,

当n=0时,=2n+1.故a=3时对所有自然数n均成立.

所以满足条件的a的最小值为3 

(3)由(1)知f(k)=

下面证明:

首先证明0<x<1时,

设函数g(x)=6x(x2-x)+1,0<x<1,  则.

当时,g'(x)<0;   当

故g(x)在区间(0,1)上的最小值

所以,当0<x<1时,g(x)>0,即得

由0<a<1知

 

 

【点评】本小题属于高档题,难度较大,需要考生具备扎实的数学基础和解决数学问题的能力.主要考查了导数的应用、不等式、数列等基础知识;考查了思维能力、运算能力、分析问题与解决问题的能力和创新意识能力;且又深层次的考查了函数、转换与化归、特殊与一般等数学思维方法.