题目内容
已知函数f(x)=
有3个零点,则实数a的取值范围是 .
|
分析:由题意可得,a>0 且 y=ax2+2x+1在(-2,0)上有2个零点,再利用二次函数的性质求得a的范围.
解答: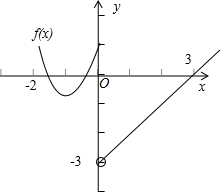 解:∵函数f(x)=
解:∵函数f(x)=
有3个零点,
∴a>0 且 y=ax2+2x+1在(-2,0)上有2个零点,
∴
,
解得
<a<1,
故答案为:(
,1).
 解:∵函数f(x)=
解:∵函数f(x)=
|
∴a>0 且 y=ax2+2x+1在(-2,0)上有2个零点,
∴
|
解得
| 3 |
| 4 |
故答案为:(
| 3 |
| 4 |
点评:本题主要考查函数零点的定义,二次函数的性质应用,属于基础题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目