题目内容
已知两条直线l1:x+my+6=0l2:(m-2)x+3y+2m=0m为何值时,l1与l2
①相交;
②平行;
③垂直.
①相交;
②平行;
③垂直.
分析:①利用两条直线相交时,由方程组得到的一次方程有唯一解,一次项的系数不等于0.
②利用两直线平行时,一次项系数之比相等,但不等于常数项之比,求出m的值.
③当两条直线垂直时,斜率之积等于-1,解方程求出m的值.
②利用两直线平行时,一次项系数之比相等,但不等于常数项之比,求出m的值.
③当两条直线垂直时,斜率之积等于-1,解方程求出m的值.
解答:解:①当l1和l2相交时,1×3-(m-2)m≠0,
由1×3-(m-2)m=0,m2-2m-3=0,∴m=-1,或m=3,∴当m≠-1且m≠3时,l1和l2相交.
②∵m=0时,l1不平行l2,l1∥l2?
=
≠
,解得m=-1.
③l1⊥l2 时,1×(m-2)+m×3=0,m=
,∴当m=
时,l1⊥l2.
由1×3-(m-2)m=0,m2-2m-3=0,∴m=-1,或m=3,∴当m≠-1且m≠3时,l1和l2相交.
②∵m=0时,l1不平行l2,l1∥l2?
| m-2 |
| 1 |
| 3 |
| m |
| 2m |
| 6 |
③l1⊥l2 时,1×(m-2)+m×3=0,m=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查两直线相交、垂直、平行的条件,体现了转化的数学思想.

练习册系列答案
相关题目
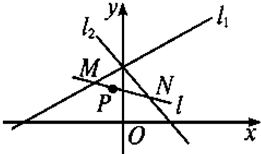 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.