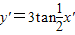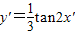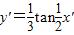题目内容
将曲线y=tanx所如下变换:
,得到的曲线方程为( )
|
分析:利用变换可得坐标之间的关系,代入曲线y=tanx,可得结论.
解答:解:∵变换:
,∴
代入曲线y=tanx,可得3y′=tan2x′,∴y′=
tan2x′
故选B.
|
|
代入曲线y=tanx,可得3y′=tan2x′,∴y′=
| 1 |
| 3 |
故选B.
点评:本题考查伸缩变换,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 ,得到的曲线方程为
,得到的曲线方程为


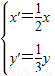 ,得到的曲线方程为( )
,得到的曲线方程为( )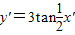
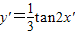
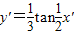
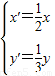 ,得到的曲线方程为( )
,得到的曲线方程为( )