题目内容
证明以下命题:
(1)对任一正整数![]() ,都存在正整数
,都存在正整数![]() ,使得
,使得![]() 成等差数列;
成等差数列;
(2)存在无穷多个互不相似的三角形![]() ,其边长
,其边长![]() 为正整数且
为正整数且![]() 成等差数列.
成等差数列.
证明:
(1)易知![]() 成等差数列,则
成等差数列,则![]() 也成等差数列,所以对任一正整数
也成等差数列,所以对任一正整数![]() ,都存在正整数
,都存在正整数![]() ,使得
,使得![]() 成等差数列.
成等差数列.
(2)若![]() 成等差数列,则有
成等差数列,则有![]() ,
,
即![]() ……①
……①
选取关于![]() 的一个多项式,例如
的一个多项式,例如![]() ,使得它可按两种方式分解因式,由于
,使得它可按两种方式分解因式,由于
![]()
因此令 ,可得
,可得
易![]() 验证
验证![]() 满足①,因此
满足①,因此![]() 成等差数列,
成等差数列,
当![]() 时,有
时,有![]() 且
且![]()
因此以![]() 为边长可以构成三角形,将此三角形记为
为边长可以构成三角形,将此三角形记为![]() .
.
其次,任取正整数![]() ,假若三角形
,假若三角形![]() 与
与![]() 相似,则有:
相似,则有:
![]()
据此例性质有:

所以![]() ,由此可得
,由此可得![]() ,与假设
,与假设![]() 矛盾,即任两个三角形
矛盾,即任两个三角形![]() 与
与![]()
![]() 互不相似,所以存在无穷多个互不相似的三角形
互不相似,所以存在无穷多个互不相似的三角形![]() ,其边长
,其边长![]() 为正整数且以
为正整数且以![]() 成等差数列.
成等差数列.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ,都存在正整数
,都存在正整数 ,使得
,使得 成等差数列;
成等差数列; ,其边长
,其边长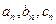 为正整数且
为正整数且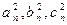 成等差数列.
成等差数列.  成等差数列。
成等差数列。 ,其边长
,其边长 为正整数且
为正整数且 成等差数列。
成等差数列。