题目内容
已知函数f(x)＝ax3－x2＋cx(a≠0)的图像如下所示，它与x轴仅有两个交点O(0,0)和A(xA,0)(xA>0)．
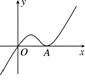
(1)证明：常数c≠0；
(2)如果xA＝
，求函数f(
x)的解析式．
解析 (1)反证法：假设c＝0，则y＝x2(ax－1)．
∴xA＝
>0.
当x>xA时，f(x)>0；当x<xA时，f(x)<0.这与图像所给的当0<x<xA时f(x)>0矛盾，∴c≠0.
(2)f(x)＝x(ax2－x＋c)．
∵函数的图像与x轴有且仅有两个公共点，
∴ax2－x＋c＝0有两个相等的实数根x＝.
∴＝＋＝1且Δ＝1－4ac＝0，解得
故所求函数为f(x)＝x3－x2＋
x.
练习册系列答案
阅读快车系列答案
相关题目
(a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x1＝3，x2＝4.
.
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
)