题目内容
定义在(1,+∞)上的函数f(x)=log2(x+ +5)的最小值是________.
+5)的最小值是________.
3
分析:由于函数f(x)= ≥log28=3,当且仅当 x-1=1 时,等号成立,从而得出结论.
≥log28=3,当且仅当 x-1=1 时,等号成立,从而得出结论.
解答:定义在(1,+∞)上的函数f(x)= ≥log28=3,当且仅当 x-1=1 时,
≥log28=3,当且仅当 x-1=1 时,
等号成立,故函数f(x)=log2(x+ +5)的最小值是3,
+5)的最小值是3,
故答案为:3.
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.
分析:由于函数f(x)=
 ≥log28=3,当且仅当 x-1=1 时,等号成立,从而得出结论.
≥log28=3,当且仅当 x-1=1 时,等号成立,从而得出结论.解答:定义在(1,+∞)上的函数f(x)=
 ≥log28=3,当且仅当 x-1=1 时,
≥log28=3,当且仅当 x-1=1 时,等号成立,故函数f(x)=log2(x+
 +5)的最小值是3,
+5)的最小值是3,故答案为:3.
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
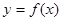 是定义在(1,4)上单调递减函数,且
是定义在(1,4)上单调递减函数,且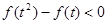 ,求
,求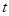 的取值范围。
的取值范围。 是定义在[2a+1,a+5]上的偶函数,则a的值为
是定义在[2a+1,a+5]上的偶函数,则a的值为