题目内容
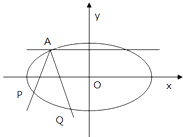
【题目】设圆x2+y2=12与抛物线x2=4y相交于A，B两点，F为抛物线的焦点，若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点，从左至右依次为P1 ， P2 ， P3 ， P4 ， 则|P1P2|+|P3P4|的值 ， 若直线m与抛物线相交于M，N两点，且与圆相切，切点D在劣弧 
上，则|MF|+|NF|的取值范围是 ．
【答案】5 
；[2+4 
，22]
【分析】联立圆和抛物线的方程求出交点坐标即可判断直线和圆分别交于四点，根据已知利用四点的横坐标表示结合韦达定理代入上式即可的结果。设出直线方程即得交点坐标再利用点的纵坐标表示出|MF|+|NF|即得到关于k与b的函数式，再结合斜率的值得到k的取值范围，再把k的取值范围代入上式求出其取值范围即可。
【解析】解：由 
，得 
或 
，
即A（﹣2 ，2），B（2 ，2）．
∵点F坐标为（0，1），∴kFB= 
，∴kl＞kFB，
所以直线l与圆交于P1、P3两点，与抛物线交于P2、P4两点，
设P1（x1，y1），P2（x2，y2），P3（x3，y3），P4（x4，y4）
把直线l方程：y=x+1代入x2=4y，得x2﹣4x﹣4=0，∴x2+x4=4；
把直线l方程：y=x+1代入x2+y2=12，得2x2+2x﹣11=0，∴x1+x3=﹣1
∴|P1P2|+|P3P4|= [（x2﹣x1）+（x4﹣x3）]= [（x2+x4）﹣（x1+x3）]=5
所以|P1P2|+|P3P4|的值等于5 ．
设直线m的方程为y=k+b（b＞0），
代入抛物线方程得x2﹣4kx﹣4b=0，
设点M（x1，y1），N（x2，y2），则x1+x2=4k，
则y1+y2=k（x1+x2）+2b=4k2+2b，
∵直线m与该圆相切，∴ 
= 
，即 
，
又|MF|=y1+1，|NF|=y2+1，
∴|MF|+|NF|=y1+y2+2=4k2+2b+2= 
∵kOA=﹣ 
，kOB= ，∴分别过A、B的圆的切线的斜率为 ，﹣ ．
∴k∈[﹣ ， ]，∴0≤k2≤2，∴0≤ 
﹣1≤12，
∵b＞0，∴b∈[2 ，6]
所以|MF|+|NF|的取值范围为[2+4 ，22]．
所以答案是：5 ；[2+4 ，22]．
