题目内容
已知函数 的导函数
的导函数 的图象如图所示,那么函数
的图象如图所示,那么函数 的图象最有可能的是( )
的图象最有可能的是( )
A
解析试题分析:∵当 (x)>0时
(x)>0时 (x)单调递增,当
(x)单调递增,当 (x)<0时
(x)<0时 (x)单调递减
(x)单调递减
∴当x 时
时 (x)单调递增,当x
(x)单调递增,当x 时
时 (x)单调递增,当x
(x)单调递增,当x 时
时 (x)单调递增.
(x)单调递增.
考点:导数在函数单调性中的应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
定义: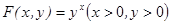 ,已知数列
,已知数列 满足:
满足:
 ,若对任意正整数
,若对任意正整数 ,都有
,都有
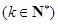 成立,则
成立,则 的值为( )
的值为( )
A. | B. | C.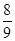 | D. |
函数 是( )
是( )
A.最小正周期为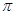 的偶函数 的偶函数 |
B.最小正周期为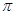 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则它们共同具有的性质是( )
| A.周期性 | B.偶函数 | C.奇函数 | D.无最大值 |
已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足2a=3,3b=2.则n的值是 ( ).
| A.-2 | B.-1 | C.0 | D.1 |
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( ).
| A.-2≤t≤2 | B.- ≤t≤ ≤t≤ |
| C.t≤-2或t=0或t≥2 | D.t≤- 或t=0或t≥ 或t=0或t≥ |
已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-3,则f(-2)=( ).
| A.1 | B.-1 | C. | D.- |
已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2]时,f(x)=ex-1,则f(2 013)+f(-2 014)=( ).
| A.1-e | B.e-1 |
| C.-1-e | D.e+1 |
 (0<a<1)的图象的大致形状是 ( ).
(0<a<1)的图象的大致形状是 ( ).