题目内容
已知正三角形PAD所在的平面与直角梯形ABCD垂直，且AB⊥AD，AB∥CD，且AD=DC=2，AB=4.
（Ⅰ）求证：AB⊥PD
（Ⅱ）求点C到平面PAB的距离
（Ⅲ）在线段PD上是否存在一点M，使得AM∥平面PBC
（Ⅰ）求证：AB⊥PD
（Ⅱ）求点C到平面PAB的距离
（Ⅲ）在线段PD上是否存在一点M，使得AM∥平面PBC
证明：（Ⅰ）
(Ⅱ)由
即
（或过D作PA的垂线，求垂线段的长）
（Ⅲ）假设PD上存在点M，使得AM∥平面PBC.
在平面PDC内过点M作MN∥DC交PC于N,连接BN,
则
又
∴平面AMNB是平行四边形
∴MN=AB这与
矛盾，
即在线段PD上不存在一点M，使得AM∥平面PBC.
(Ⅱ)由
即（或过D作PA的垂线，求垂线段的长）
（Ⅲ）假设PD上存在点M，使得AM∥平面PBC.
在平面PDC内过点M作MN∥DC交PC于N,连接BN,
则
又∴平面AMNB是平行四边形
∴MN=AB这与
矛盾，即在线段PD上不存在一点M，使得AM∥平面PBC.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
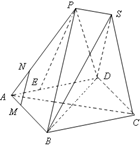已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
（2012•开封二模）如图，已知四棱锥P-ABCD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，∠DAB=60°．
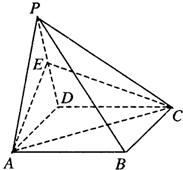如图，已知正三角形PAD，正方形ABCD，平面PAD⊥平面ABCD，E为PD的中点．
如图，已知正三角形PAD，正方形ABCD，平面PAD⊥平面ABCD，E为PD的中点．