题目内容
已知数列{an}满足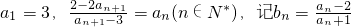 .
.
(Ⅰ)求数列{bn}的通项公式.
(Ⅱ)若(4n-1)an≥t•2n+1-17对任意n∈N*恒成立,求实数t的取值范围;
(Ⅲ)记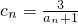 ,求证:
,求证: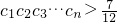 .
.
解:(Ⅰ)∵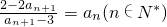 ,∴
,∴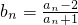 =
=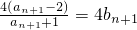 ,
,
∴
∵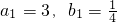
∴数列{bn}是以 为首项,
为首项, 为公比的等比数列
为公比的等比数列
∴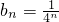 ;
;
(Ⅱ)∵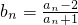 ,∴
,∴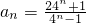
∵(4n-1)an≥t•2n+1-17对任意n∈N*恒成立,
∴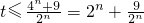 对任意n∈N*恒成立
对任意n∈N*恒成立
∵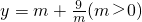 在(0,3)上单调递减,在(3,+∞)上单调递增
在(0,3)上单调递减,在(3,+∞)上单调递增
∴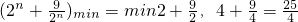
∴
∴实数t的取值范围是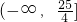 ;
;
(Ⅲ)∵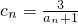 =
=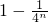 ,
,
猜想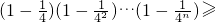
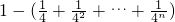
用数学归纳法证明:
①n=1时,左边= =右边;n=2时,左边=
=右边;n=2时,左边=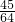 ,右边=
,右边=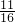 ,左边>右边;
,左边>右边;
②假设n=k(k≥2)时结论成立,即
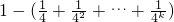
则n=k+1时,左边=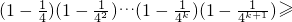
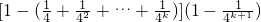
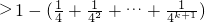 =右边
=右边
由①②知,猜想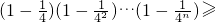
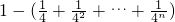 成立
成立
又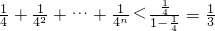
∴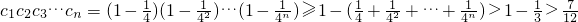
∴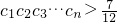
分析:(Ⅰ)根据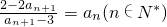 ,可得
,可得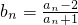 =
=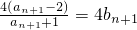 ,从而可得数列{bn}是以
,从而可得数列{bn}是以 为首项,
为首项, 为公比的等比数列,故可求数列{bn}的通项公式;
为公比的等比数列,故可求数列{bn}的通项公式;
(Ⅱ)将(4n-1)an≥t•2n+1-17对任意n∈N*恒成立,等价于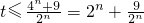 对任意n∈N*恒成立
对任意n∈N*恒成立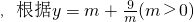 在(0,3)上单调递减,在(3,+∞)上单调递增,可求右边函数的最小值,从而可求实数t的取值范围;
在(0,3)上单调递减,在(3,+∞)上单调递增,可求右边函数的最小值,从而可求实数t的取值范围;
(Ⅲ)因为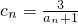 =
=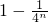 ,为了证明结论,首先猜想并证明
,为了证明结论,首先猜想并证明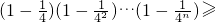
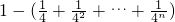 ,利用
,利用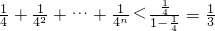 ,即可证得结论.
,即可证得结论.
点评:本题以数列递推式为载体,考查数列的通项,考查恒成立问题,考查不等式的证明,解题的关键是恒成立问题的等价转化,及数列的特殊性,第(Ⅲ)难度较大.
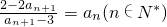 ,∴
,∴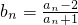 =
=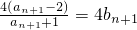 ,
,∴

∵
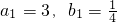
∴数列{bn}是以
 为首项,
为首项, 为公比的等比数列
为公比的等比数列∴
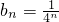 ;
;(Ⅱ)∵
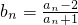 ,∴
,∴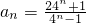
∵(4n-1)an≥t•2n+1-17对任意n∈N*恒成立,
∴
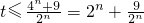 对任意n∈N*恒成立
对任意n∈N*恒成立∵
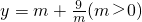 在(0,3)上单调递减,在(3,+∞)上单调递增
在(0,3)上单调递减,在(3,+∞)上单调递增∴
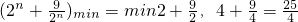
∴

∴实数t的取值范围是
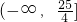 ;
;(Ⅲ)∵
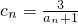 =
=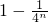 ,
,猜想
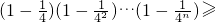
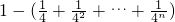
用数学归纳法证明:
①n=1时,左边=
 =右边;n=2时,左边=
=右边;n=2时,左边=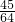 ,右边=
,右边=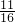 ,左边>右边;
,左边>右边;②假设n=k(k≥2)时结论成立,即

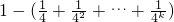
则n=k+1时,左边=
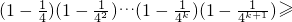
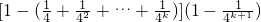
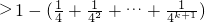 =右边
=右边由①②知,猜想
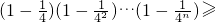
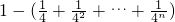 成立
成立又
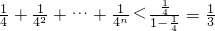
∴
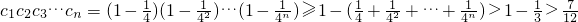
∴
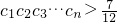
分析:(Ⅰ)根据
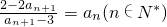 ,可得
,可得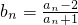 =
=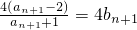 ,从而可得数列{bn}是以
,从而可得数列{bn}是以 为首项,
为首项, 为公比的等比数列,故可求数列{bn}的通项公式;
为公比的等比数列,故可求数列{bn}的通项公式;(Ⅱ)将(4n-1)an≥t•2n+1-17对任意n∈N*恒成立,等价于
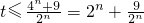 对任意n∈N*恒成立
对任意n∈N*恒成立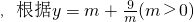 在(0,3)上单调递减,在(3,+∞)上单调递增,可求右边函数的最小值,从而可求实数t的取值范围;
在(0,3)上单调递减,在(3,+∞)上单调递增,可求右边函数的最小值,从而可求实数t的取值范围;(Ⅲ)因为
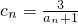 =
=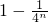 ,为了证明结论,首先猜想并证明
,为了证明结论,首先猜想并证明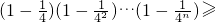
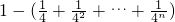 ,利用
,利用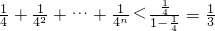 ,即可证得结论.
,即可证得结论.点评:本题以数列递推式为载体,考查数列的通项,考查恒成立问题,考查不等式的证明,解题的关键是恒成立问题的等价转化,及数列的特殊性,第(Ⅲ)难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目