题目内容
已知函数f（x）=a（x+a）（x-2a+1），g（x）=2x-4满足条件：对任意x∈R，“f（x）＜0”与“g（x）＜0”中至少有一个成立，则实数a的取值范围是 ．
分析：经分析，x＜2，“g（x）＜0”成立，进而得到a（x+a）（x-2a+1）＜0对x≥2均成立，
故得到a满足的条件，解出即可．
故得到a满足的条件，解出即可．
解答：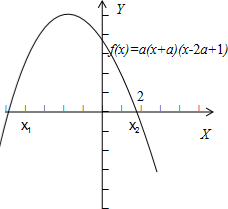
解：∵g（x）=2x-4＜0，得x＜2，故对x≥2时，“g（x）＜0”不成立，
从而对任意x≥2，“f（x）＜0”恒成立，
由于a（x+a）（x-2a+1）＜0对任意x≥2恒成立，如图所示，
则必满足
，故
解得-2＜a＜0
则实数a的取值范围是 （-2，0）
故答案为 （-2，0）
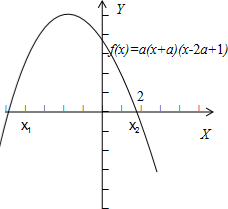解：∵g（x）=2x-4＜0，得x＜2，故对x≥2时，“g（x）＜0”不成立，从而对任意x≥2，“f（x）＜0”恒成立，
由于a（x+a）（x-2a+1）＜0对任意x≥2恒成立，如图所示，
则必满足
|
|
则实数a的取值范围是 （-2，0）
故答案为 （-2，0）
点评：本题考查了不等式的解法亦即函数的恒成立问题，属于基础题．
练习册系列答案
相关题目