Question

若六棱锥S—ABCDEF的侧棱SA的长是10 cm ，底面ABCDEF是边长为8 cm的正六边形，且棱锥的高过正六边形的中心，这个棱锥被平行于底面的平面所截，截得的截面面积是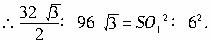，求这个截面和底面之间的距离和侧面积.

Answer 1

解析：如题图，设SO为这个棱锥的高，它与截面相交于O₁，则O为六边形ABCDEF的中心.?

∵AB=8 cm ，且ABCDEF为正六边形,?

∴AO=AB=8 cm .又SA=10 cm ,∴SO=6 cm .?

∵,?

∴.?

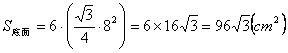∴SO₁²=4.∴SO₁=2(cm).?

∴SO-SO₁=6-2=4(cm).?

设小棱锥的侧面积为S₁，大棱锥的侧面积为S₂，?

则.?

∵六棱锥S—ABCDEF的斜高h₁为，?

∴.∴.?

∴截面和底面之间的侧面积为S₂-S₁= cm².?

截面和底面之间的距离为4 cm .