题目内容

（2011•杭州一模）若（x-1）8=a0+a1（1+x）+a2（x+1）2+…+a8（1+x）8，则a6=（　　）
分析：依题意，（x-1）8=[（x+1）-2]8，a6=
C
2
8
•（-2）2，从而可得答案．
解答：解：∵（x-1）8=a0+a1（1+x）+a2（x+1）2+…a8（1+x）8，
又（x-1）8=[（x+1）-2]8，
∴a6=
C
2
8
•（-2）2=28×4=112．
故选A．
点评：本题考查二项式定理的应用，将（x-1）8转化为[（x+1）-2]8是关键，考查二项展开式的通项公式的应用，属于中档题．
练习册系列答案
相关题目
（2011•杭州一模）设α∈(0， 
π
2
)．若tanα=
1
3
，则cosα=
3
10
10
3
10
10
．
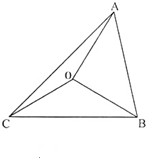（2011•杭州一模）已知点O为△ABC的外心，角A，B，C的对边分别满足a，b，c，
（I）若3
OA
+4
OB
+5
OC
=
0
，求cos∠BOC的值；
（II）若
CO
•
AB
=
BO
•
CA
，求
b2+c2
a2
的值．
（2011•杭州一模）设函数f（x）=x-2sinx是区间[t，t+
π
2
]上的增函数，则实数t的取值范围是（　　）
（2011•杭州一模）已知等比数列{an}的公比大于1，Sn是数列{an}的前n项和，S3=39，且a1，
2
3
a2，
1
3
a3依次成等差数列．
（Ⅰ）求数列{an}的通项公式；
（II）若数列{bn}满足：b1=3，bn=an（
1
a1
+
1
a2
+…+
1
an-1
）（n≥2），求数列{bn}的前n项和Tn．
（2011•杭州一模）设函数f（x）=
2+log3x，x＞0
3-log2(-x)，x＜0
，则f（
3
）+f（-
2
）=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网