Question

某电脑公司有3名产品推销员，其工作年限与年推销金额数据如下表，由表中数据得出线性回归方程为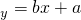．若第4名推销员的工作年限为6年，则估计他的年推销金额为多少万元？

推销员编号	1	2	3
工作年限x（年）	3	5	10
推销金额y（万元）	2	3	4

1. A.
   2
2. B.
   3
3. C.
   3.3
4. D.
   3.5

Answer 1

B
分析：根据所给的两组数据，做出x和y的平均数，写出这组数据的样本中心点，根据线性回归方程一定过样本中心点，得到线性回归直线一定过的点的坐标．最后根据第4名推销员的工作年限为6年，即当x=6时，把自变量的值代入线性回归方程，得到y的预报值，即估计出第4名推销员的年推销金额．
解答：设所求的线性回归方程为y=bx+a，
由于==6，=3，
∴这组数据的样本中心点是（6，3）
∵线性回归方程过样本中心点，
∴线性回归方程一定过点（6，3）
若第4名推销员的工作年限为6年，则估计他的年推销金额为3万元．
故选B．
点评：本题考查线性回归方程的意义，线性回归方程一定过样本中心点，本题解题的关键是正确求出样本中心点，题目的运算量比较小，是一个基础题．