题目内容
已知函数f(x)=x2+2x+alnx.(1)若f(x)在区间(0,1］上恒为单调函数，求实数a的取值范围；
(2)当t≥1时，不等式f(2t-1)≥2f(t)-3恒成立，求实数a的范围.
解：f′(x)=2x+
+2,
(1)若f(x)是(0,1］上的增函数，则f′(x)=2x+
+2≥0.
在(0,1］上恒成立，即a≥-2x2-2x.
令g(x)=-2x2-2x,x∈(0,1］，∴g(x)max=0,∴a≥0.
若f(x)在(0,1］上单调递减，则f′(x)=2x+
+2≤0.
在x∈(0,1］上恒成立，
即a≤-2x2-2x,x∈(0,1］，g(x)=-2x2-2x,当x∈(0,1］,g(x)min=-4.∴a≤-4,
∴当f(x)在(0,1］恒为单调函数时，a≥0或a≤-4.
(2)∵f(x)=x2+2x+alnx，由f(2t-1)≥2f(t)-3得
(2t-1)2+2(2t-1)+aln(2t-1)≥2(t2+2t+alnt)-3,
化简为：2(t-1)≥aln
.①
∵当t＞1时，有t2＞2t-1,∴ln
＞0.
故a≤
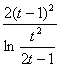,②
构造函数m(x)=ln(1+x)-x (x＞-1),
m′(x)=
-1=
,
则m(x)在x=0取得极大值，同时也是最大值，故m(x)≤m(0),
从而ln(1+x)≤x在x＞-1时恒成立，故
ln
=ln［1+
］≤
＜(t-1)2,③
当t＞1时恒成立，而t=1时，③式取得“=”,
∴ln
≤(t-1)2,④
当t≥1时恒成立，因此由②③④可知实数a的范围为a≤2.
