题目内容
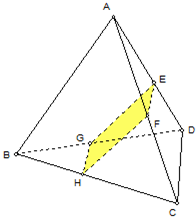
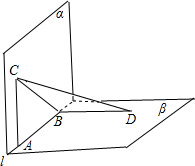
已知二面角α-l-β等于90°，A、B是棱l上两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，已知AB=5，AC=3，BD=4，则CD与平面α所成角的正弦值为______．
连接BC，则
∵二面角α-l-β等于90°，BD⊥l，
∴∠BCD就是CD与平面α所成角．
在Rt△ABC中，AB=5，AC=3，∴BC=
，
在Rt△DBC中，BD=4，∴CD=5
，∴sin∠BCD=
=
．
故答案为：
．
∵二面角α-l-β等于90°，BD⊥l，
∴∠BCD就是CD与平面α所成角．
在Rt△ABC中，AB=5，AC=3，∴BC=
| 34 |
在Rt△DBC中，BD=4，∴CD=5
| 2 |
| BD |
| CD |
2
| ||
| 5 |
故答案为：
2
| ||
| 5 |
练习册系列答案
阅读快车系列答案
相关题目
