题目内容
函数f(x)=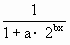 的定义域为R,且
的定义域为R,且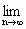 f(-n)=0(n∈N).
f(-n)=0(n∈N).
(1)求证:a>0,b<0;
(2)(文)若f(1)=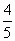 且f(0)=
且f(0)=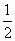 ,求证:f(1)+f(2)+…+f(n)>n+
,求证:f(1)+f(2)+…+f(n)>n+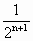 -
-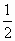 (n∈N).
(n∈N).
(理)若f(1)=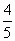 ,且f(x)在[0,1]上的最小值为
,且f(x)在[0,1]上的最小值为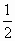 ,求证:f(1)+f(2)+…+f(n)>n+
,求证:f(1)+f(2)+…+f(n)>n+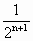 -
-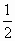 (n∈N).
(n∈N).
答案:
解析:
解析:
|
(1)∵f(x)定义域为R,∴1+a2bx≠0,即a≠-2-bx而x∈R,∴a≥0. 若a=0,则f(x)=1与 ∴ ∴2-b>1即b<0,故a>0,b<0. (2)(文)∵f(0)= ∴b=-2.∴f(x)= 当k∈N时,f(k)=1- (理)由(1)知f(x)在[0,1]上为增函数,∴f(0)= f(1)= ∴f(x)= 当k∈N时,f(k)=1- |

练习册系列答案
相关题目
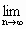 f(-n)=0矛盾,∴a>0,
f(-n)=0矛盾,∴a>0,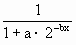 =
=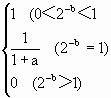
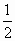 ,即
,即 =
=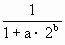 =
=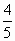 ,∴2b=
,∴2b=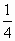 ,
,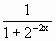 =
=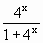 =1-
=1-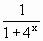 .
.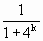 >1-
>1-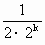 ∴f(1)+f(2)+f(3)+…+f(n)>n-(
∴f(1)+f(2)+f(3)+…+f(n)>n-(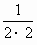 +
+ +
+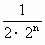 )=n+
)=n+ -
-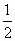 .
.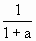 =
=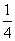 ,∴b=-2.
,∴b=-2.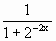 =
= 的图象上有两个关于直线x+y=3对称的不动点,求a的值.
的图象上有两个关于直线x+y=3对称的不动点,求a的值.